Unit 6: Wave motion
| Unit 6 | Wave motion |
|---|---|
| 6.1 | Define and understand progressive wave |
| 6.2 | Write progressive wave in mathematical form |
| 6.3 | Discuss the condition under which stationary waves can be formed |
| 6.4 | Write stationary wave in mathematical form |
| 6.5 | Calculate the frequency, amplitude, velocity, time period, etc of the progressive wave |
| 6.6 | Find an expression for stationary wave using two progressive wave |
 |
| Unit 6: Wave Motion |
Wave:
Wave is a continuous transfer of disturbance from one part of a medium to another through successive vibrations of the particles of the medium about their mean positions. In a wave motion, there is energy transfer without matter transport.
Types of wave:
a) Mechanical wave / Elastic wave
The waves which require a material medium for their propagation are called Mechanical waves. They cannot transmit in a vacuum. Eg. Sound waves, Vibration in a stretched string, ripples on a pond, etc.
b) Electromagnetic Wave / Non-mechanical wave
The waves which do not require a material medium for their propagation are called Electromagnetic waves. They can transmit in a vacuum. Eg. Lightwaves, X-rays, Gamma rays, etc.
c) Matter Waves
The waves that are associated with the motion of the particle of an atomic or subatomic size such as electrons, protons, etc are called Matter waves.
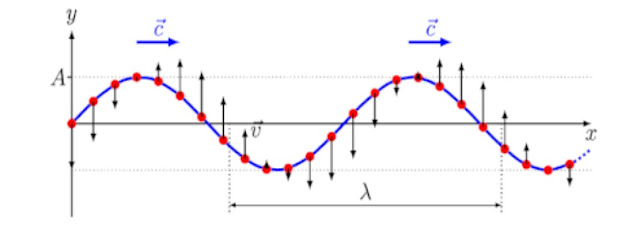
Wave and oscillatory motion:
A wave is a disturbance that travels form one region of a medium to another. Here the disturbance represents the change in pressure, density, or displacement of the particles of the medium about their equilibrium position.
Periodic back and forth ( to and fro ) motion of particles of the medium about their mean position i.e. oscillatory motion.
That is Simple Harmonic Motion.
The corresponding wave is called a Harmonic wave or sinusoidal wave.
Some general terms of SHM
(a)Displacement (y):
The displacement of a particle executing SHM at any time ‘t’ is the distance it has moved from the mean position at that time.
y = A sin ωt
where A is the amplitude of SHM and is defined as the maximum displacement of the particle on either side of the mean position.
(b) Particle velocity (u):
u = 𝑑𝑦 / 𝑑𝑡 = A ω cos ωt
( Particle velocity is the function of time)
(c) Phase angle (θ ):
The angular displacement of the particle in SHM in time ‘t’ is called phase angle and is measured in radians in the SI unit.
θ = ωt
Some important terms associated with the wave motion
(a) Crest:
The position of maximum displacement of the particles of a medium above the equilibrium position
(b) Trough:
The position of maximum displacement of the particles of a medium below the equilibrium position
(c) Amplitude (A):
The maximum displacement of particles in a medium about their mean position.
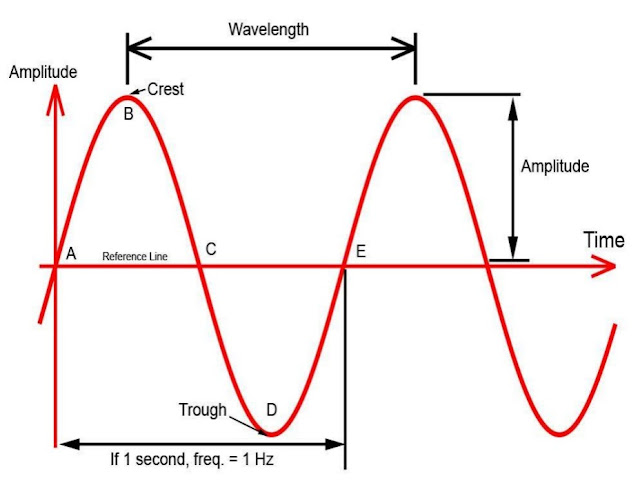
(d) Wavelength (λ):
The distance traveled by the wave in one complete cycle.
(e) Wave Frequency (f):
The number of oscillations/ vibrations/ cycles per second. It is measured in cycles/sec or hertz.
(f) Time Period (T):
The time in which a particle of medium completes one vibration about its mean position
f = 1 / 𝑇
(g) Wave velocity(v):
Distance traveled by the wave per unit time
v = λ / 𝑇 = f λ
Characteristics of wave motion
- Wave motion is the disturbance traveling through a medium.
- When a wave passes through a medium, only the energy is transferred from one particle to another. The particle of the medium executes vibrations only about their mean position. i.e. there is no net displacement of the particle.
- To transfer the energy from one place to another in the form of a wave, the medium should possess the property of elasticity and inertia.
- Particle velocity is the function of time, so it is different at different points of displacement. But the wave velocity is constant in a medium.
- A vibrating particle of the medium possesses both kinetic and potential energies.
Types of Mechanical waves
On the basis of the vibration of particles of the medium, mechanical waves are categorized into two types:
- Transverse Wave
- Longitudinal Wave
a) Transverse wave
The wave in which the particles of the medium vibrate about their mean position perpendicularly to the direction of propagation of the wave is called a Transverse wave. Such wave propagates in the form of a crest and trough. These waves can propagate on only those mediums which can sustain shearing stress. Eg. Waves produced on plugging a stretched string.

b) Longitudinal wave
The wave in which the particles of the medium vibrate along the direction of propagation of the wave is called a Longitudinal wave. Such wave propagates in the form of compression and rarefaction. These waves can propagate on those mediums which can sustain compressive stress. For eg. Sound waves, Seismic P-waves, etc. These waves are also called Pressure Waves.

Types of Oscillations and Resonance
1. Free Oscillation:
The oscillations, in which external forces are absent is called Free Oscillation. It will oscillate forever with constant amplitude, frequency and energy. The frequency of a body executing free oscillation is called its natural frequency. Eg: Oscillation of simple pendulum in a vacuum
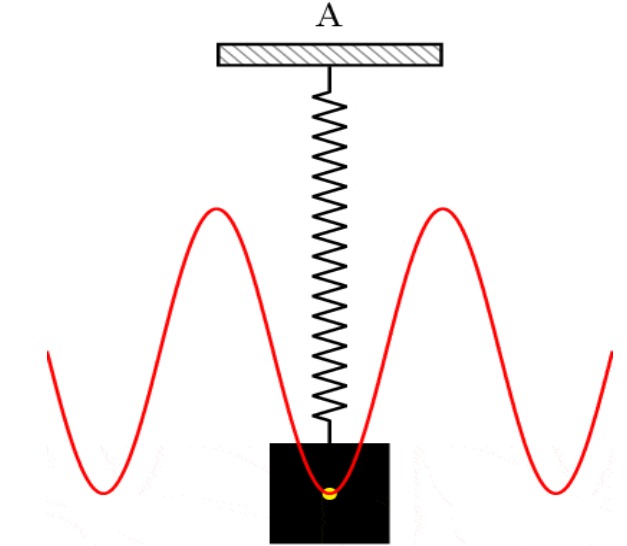
2. Damped Oscillation:
The oscillation, in which the amplitude of oscillation gradually decreases and finally becomes zero due to the presence of external resistive force is called Damped Oscillation. Eg: Motion of a simple pendulum in the air
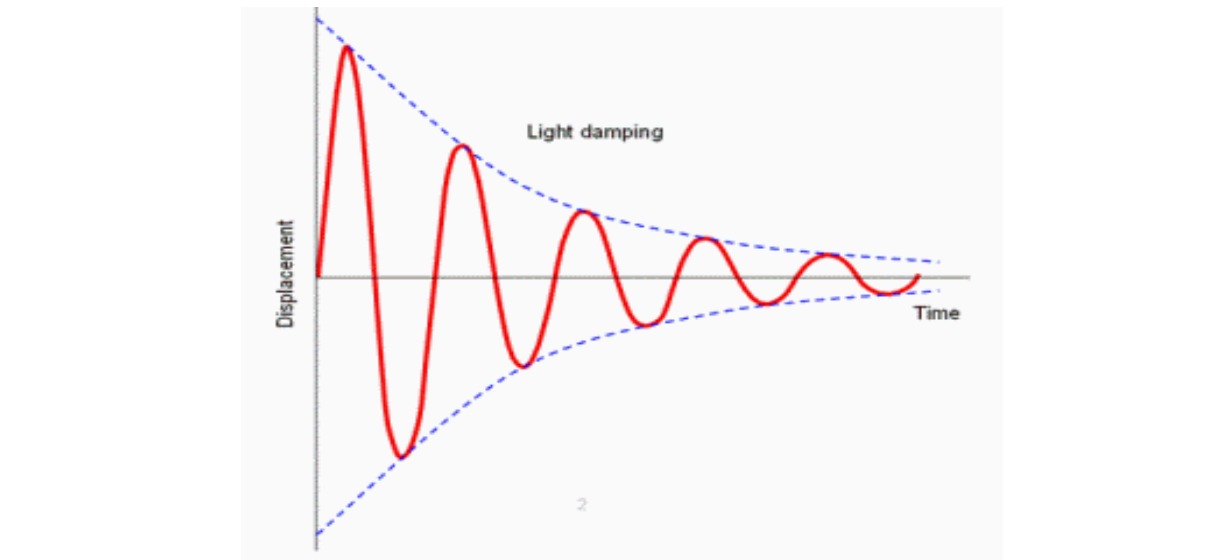
3. Forced Oscillation:
In order to keep the amplitude constant in damped oscillation, the external periodic force must be applied and the oscillation is called Forced Oscillation.
Resonance:
In forced Oscillation, when the forcing frequency i.e. frequency of external periodic force coincides with the natural frequency of the oscillating body, it oscillates with maximum amplitude. This oscillation is called resonant oscillation and the phenomenon is called Resonance.
Some examples of Resonance:
- A child on a swing is driven by a parent at the swing’s natural frequency to achieve maximum amplitude.
- Sometimes, the glass of the windows of a house are found to break when large-sounding bodies like airplane pass near the house.
- During earthquake, buildings with natural frequencies close to the frequency of seismic wave triggered by the earthquake are most susceptible to damage.
- A tuned circuit in a radio or TV receiver responds strongly to waves having frequencies near it’s resonant frequency among numerous frequencies received from different broadcasting stations. So we can tune a particular station and reject others.
- Resonance phenomena in some mechanical systems can be destructive. For Example: Soldiers marching over a bridge.
- Many opera singers are able to break a crystal glass by singing the appropriate note.
Phase, phase difference, and path difference
The phase of a particular point in the cycle of a waveform refers to its status i.e. position and direction of oscillation in terms of angle (usually in radian) with respect to a certain reference point (generally origin) on the space.

Any two points in the cycle of a waveform are said to be in same phase if they are in the same side, equally displaced and oscillating in the same direction. These points are separated by an angle of 2π.

1 and 7,
2 and 8,
3 and 9,
4 and 10,
5 and 11,
6 and 12 are in the same phase.
Path Difference ( x ):
Linear distance between two points in a wave.
Phase Difference ( Ø ):
Difference of angular displacement of two points in a wave.
Relation between path difference (x) and phase difference (Ø )
%20and%20phase%20difference%20(%C3%98%20).jpeg)
Progressive Wave
A wave that travels continuously in a medium in the same direction without any change in its amplitude is called Progressive Wave or Travelling Wave. Progressive waves may be Transverse or Longitudinal.
 |
| source: Brainkart |
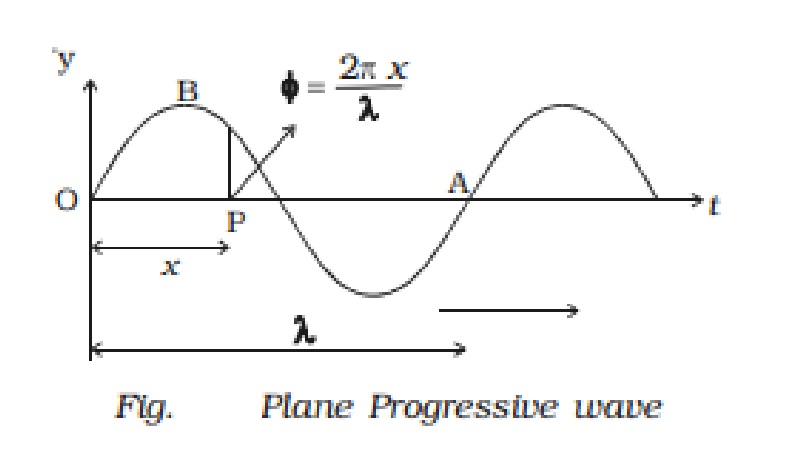
Equation of Progressive wave:
Consider a wave traveling from left to right along the x-axis as shown in the figure aside. Let a particle at origin ‘O’ is vibrating simple harmonically and its displacement at any instant of time ‘t’ is given by:
y = a sin ωt - - - - - - - (1)
where a is the amplitude of the particle and ω is its angular velocity.
Now, let us consider another particle ‘P’ at a distance ‘x’ from O. Since particle P receives the disturbance later than the particle at ‘O’, the phase of the motion of particle P lags to that of ‘O’.
If ϕ be the phase difference of the particle P, then its displacement at the given instant of time ‘t’ is given by
y = a sin (ωt – ϕ) - - - - - (2)
We know, For a path difference of ‘λ’, phase difference is 2π
For a path difference of ‘x’, phase difference is `\phi\=\frac{2\pi\x}\lambda`
`\phi\=\frac{2\pi\x}\lambda`- - - - - (3)
Substituting eq. (3) in eq. (2) gives
or, `y=a\sin\left(\omega t-kx\right)` - - - - - (5)
Where `k=\frac{2\pi}{\lambda}` is called wave number or propagation constant.
since, `\omega=\frac{2\pi}{\T}` ,eq.(4) can be expressed as
`y=a\sin\left(\frac{2\πt}T-\frac{2\pi x}\lambda\right)`
or, `y=a\sin\2pi\left(\frac tT-\frac x\lambda\right)` - - - - - (6)
or, `y=a\sin\2\pi\frac{\lambda}{\lambda}\left(\frac tT-\frac x\lambda\right)`
or, `y=a\sinfrac{2\pi}{\lambda}\left(\frac{\lambda t}T-\frac{\lambda x}\lambda\right)`
`y=a\sinfrac{2\pi}{\lambda}\left(\nu t-x\right)`- - - - - (7)
Eq. (6) and (7) are the equations of plane progressive wave.
If the wave travels from right to left then vibration at ‘P’ leads to that at O. Hence, in this case, the equation of progressive wave becomes
`y=a\sinfrac{2\pi}{\lambda}\left(\nu t+x\right)`
Formula of Wave motion
1. The displacement of a particle executing SHM at any instant t, traveling from left to right is given by:
y = a sin (ωt – kx)
2. k = 2π / λ , where k= wave no. or propagation constant
3. ω = 2 πf = 2π / T , where ω= angular velocity
4.f = 1 / T , where f = frequency and T = time period
5.Phase Difference (ϕ) = 2π / λ * Path Difference (x)
6. v = f × λ , where v= velocity and λ = wavelength
Principle of Superposition:
Principle of Superposition states that, "When two or more waves are passing through a medium at the same time, the resultant displacement at any point is equal to the vector sum of their individual displacements at that point."
If y1 , y2 , y3 , . . . ., yn be the displacements at a point due to individual waves, then the resultant displacement ‘y’ at the same time when the waves superpose to each other is given by
y = y1 + y2 + y3 + . . . . . + yn
 |
| Fig: Superposition of two identical waves travelling in opposite directions |
The principle of superposition gives rise to following important effects:
- When two waves of same frequency moving in same direction superpose, constructive interference of waves is obtained.
- When two waves of same frequency moving in opposite direction superpose, stationary waves are produced.
- When two waves of slightly different frequencies are travelling in same direction superpose, beats are produced.
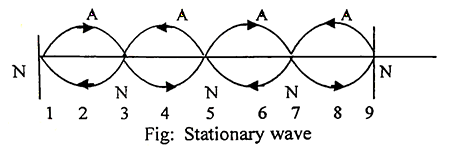
Stationary wave / Standing wave:
When two progressive wave of same amplitude and frequency travel through a medium with the same speed but in opposite direction are superposed, the resultant wave is called Stationary wave.
Stationary wave / Standing waves are called so because the wave form does not travel along in either direction.
 |
| source: qsstudy.com |
Mathematical Treatment of Stationary Waves ( Stationary wave equation )
Let us consider a plane progressive wave is travelling from left to right along X-axis. The displacement ‘y1 ’ of the wave at a distance ‘x’ from the origin is given by
𝑦1 = 𝑎 sin 𝜔𝑡 − 𝑘𝑥 - - - - - (1)
where, a is amplitude, ω is angular velocity and k is wave number.
Let another wave of the same amplitude and frequency is travelling with same velocity but in opposite direction. The displacement ‘y2 ’ of this wave in the given instant of time ‘t’ is given by
𝑦2 = 𝑎 𝑠𝑖𝑛 𝜔𝑡 + 𝑘𝑥 - - - - (2)
When these two waves are superposed, stationary wave is produced and the resultant displacement of the wave is given by principle of superposition as
y = 𝑦1 + 𝑦2 = 𝑎 𝑠𝑖𝑛 (𝜔𝑡 + 𝑘𝑥) + 𝑎𝑠𝑖𝑛 (𝜔𝑡 − 𝑘𝑥)
=`a\sin\left(\frac{\omega t+kx+\omega t-kx}2\right)\cos\left(\frac{\omega t+kx-\omega t+kx}2\right)`
= 2a 𝑠𝑖𝑛𝜔𝑡 cos(𝑘𝑥)
= 2a 𝑐𝑜𝑠𝑘𝑥 𝑠𝑖𝑛𝜔t
y = 2a 𝑐𝑜𝑠𝑘𝑥 𝑠𝑖𝑛𝜔t
y = A sin ωt - - - - - - - - - - - (3)
where, A = 2a 𝑐𝑜𝑠𝑘𝑥 is the amplitude of resultant wave
Eq. (3) is the equation of stationary wave which resembles the equation of simple harmonic motion.
Position of nodes:
Nodes are the points in the stationary wave that are permanently at rest. At nodes, A is minimum = 0 which is possible if 𝑐𝑜𝑠𝑘𝑥 = 0
or, `\cos kx=\cos\left[\left(n+\frac1\2\right)\pi\right]\;n=0,1,2\;....`
or, `\frac{2\πx}{\lambda}=\left(\ n+\frac1\2\right)\pi`
or, `\x=\left(\ n+\frac1\2\right)\frac{\lambda}2\ n=0,1,2,\;....`
`\x=\frac{\lambda}4,\frac{3\lambda}4,\frac{5\lambda}4,.......`
Hence, the distance between two consecutive nodes is `\left(\frac{3lambda}4-\frac{\lambda}4\right)=\left(\frac{5\lambda}4-\frac{3\lambda}4\right)=\frac{\lambda}2`
Position of antinodes:
Antinodes are the points in the stationary waves at which the displacement is maximum. At antinodes, A is maximum which is possible if
𝑐𝑜𝑠𝑘𝑥 = ±1
or, coskx = cos nπ ; n = 0, 1, 2. . . .
or, `\frac{2\pi}\lambda x=n\pi`
or, `\ x= n\frac{\lambda}2\; n=0,1,2,\....`
`\x=0,\frac{\lambda}2,\lambda,\frac{3\lambda}2,.......`
Hence, the distance between two consecutive antinodes is `\left(\frac{\lambda}2-0\right)=\left(\lambda-\frac{\lambda}2\right)=\frac{\lambda}2 `
Conclusion:
This concludes that the distance between two consecutive nodes or the distance between two consecutive anti nodes is equal to `\frac{\lambda}2 ` and that distance between node and anti node is `\frac{\lambda}4`.
The points other than node and anti node, the displacement decreases gradually from their maximum value at anti node to zero value at node.
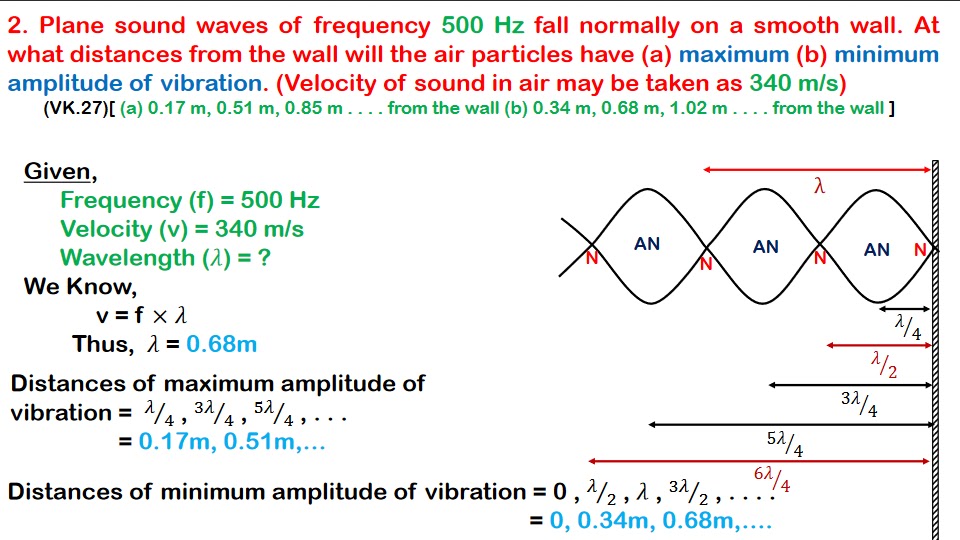
Wave Motion Numericals Class 12
These are the Physics Most Important Numericals from Wave motion unit of Class 12 Physics for NEB Exam.
Read :
91 Physics Important Question for NEB
Physics Important Question
TAGs
- Wave Motion Notes Pdf
- Class 12 Physics Notes Pdf
- Wave motion Numericals Class 12
- Class 12 Physics Book Pdf Nepal
- Physics Notes Grade 12
- Grade 12 Physics